Conversión de tasas de interés
La conversión de tasas de interés es el proceso para hallar el valor equivalente de una tasa al cambiar su tipo, nominalidad, periodicidad o forma.
Para poder entender y realizar correctamente la conversión de tasa es necesario que se tenga claridad cuáles son los Elementos de las tasas de interés los cuales como se habían mencionado en la respectiva sección de tasas de interés son los siguientes:
- Tipo: Efectiva o nominal.
- Nominalidad: Mensual, semestral, anual, etc.
- Periodicidad: Mensual, semestral, anual, etc.
- Forma: Vencida o anticipada.
- Valor: 2%, 4%, 20% etcétera.


Lo primero que se hace es definir cada elemento. Es decir, definir su tipo, definir su base nominal (en caso de ser una tasa nominal), definir su periodicidad, definir su forma y definir su valor.
Luego de haber definido cada elemento se usarán dos formatos para expresarla, uno para las tasas efectivas y otro para las tasas nominales.
La siguiente figura muestra un panorama general para poder entender que formula usar cuando se quiere hacer un cambio en cualquiera de los elementos de una tasa de interés, se debe tener presente que los cambios se deben hacer de uno en uno.
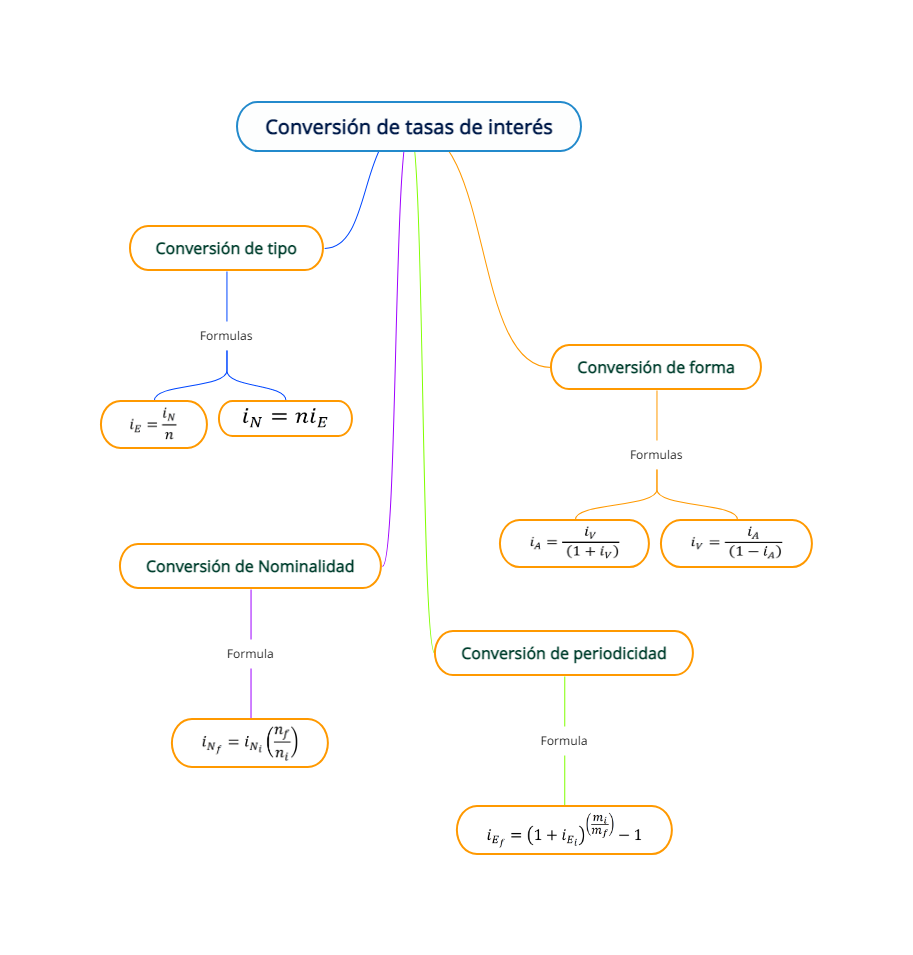

Fórmula para el cambio del tipo de tasas de interés (nominales y efectivas)
Cuando se hace el cambio del tipo, no se altera la periodicidad ni la forma, es decir que, si se tiene una tasa nominal con periodicidad mensual y forma anticipada, la tasa efectiva a la cual se va a cambiar también tendrá periodicidad mensual y forma anticipada o si se tiene una tasa efectiva con periodicidad semestral y forma vencida la tasa nominal a la cual se va a cambiar también tendrá periodicidad semestral y forma vencida.
\({i_E} = \frac{{{i_N}}}{n}\)
Fórmula para cambio de tasas de nominal a efectiva.
\({i_N} = n{i_E}\)
Fórmula para cambio de tasas de efectiva a nominal.
\({i_{E}}\), Tasa de interés efectiva.
\({i_{N}}\), Tasa de interés nominal.
\(n\), Número de veces que cabe la periodicidad en la nominalidad de la tasa nominal.
Ejemplo: Convertir una tasa del 15% nominal anual mes vencido a efectiva.
\({i_{NAMV}} = 15\% \)
\({i_{MV}} = \frac{{15\% }}{{12}} = 1,25\% \)
Se divide por 12, porque caben 12 meses (Periodicidad) en un año (Nominalidad). Vemos que ambas tasas tienen la misma periodicidad y la misma forma.
Ejemplo: Convertir una tasa del 4% trimestral anticipada a una tasa nominal semestral
\({i_{TA}} = 4\% \)
\({i_{NSTA}} = 2\left( {4\% } \right) = 8\% \)
Se multiplica por 2, porque caben 2 trimestres (Periodicidad) en un semestre (Nominalidad). Vemos que ambas tasas tienen la misma periodicidad y la misma forma.
Formula para el cambio de la nominalidad de tasas de interés (mensual, bimestral, anual, etcétera)
Cuando se hace un cambio de nominalidad, la tasa conserva la periodicidad y la forma, por ejemplo, si se tiene una tasa de interés nominal anual mes vencido, dicha formula se puede cambiar a nominal bimestral, semestral o a lo que se quiere, pero seguirá siendo una tasa con periodicidad mensual y forma vencida. El uso de esta fórmula, se puede hacer con tasas vencidas o anticipadas y obviamente se usa estrictamente con tasa nominales, nunca efectivas.
Esta fórmula se usa con muy poca frecuencia, ya que esta fórmula es la unión de las dos fórmulas anteriores usadas para el cambio del tipo de tasas de interés, sin embargo, en algunas ocasiones los profesores la usan para ejercicios de mera conversión de tasa o para confundir y colocar trampas a los estudiantes.
\({i_{{N_f}}} = {i_{{N_i}}}\left( {\frac{{{n_f}}}{{{n_i}}}} \right)\)
Fórmula para cambio de nominalidad de tasas.
\({i_{{N_i}}}\), Tasa de interés nominal inicial.
\({i_{{N_f}}}\), Tasa de interés nominal final.
\({n_i}\), Número de veces que cabe la periodicidad en la nominalidad de la tasa nominal inicial.
\({n_f}\), Número de veces que cabe la periodicidad en la nominalidad de la tasa nominal final.
Ejemplo: Convertir una tasa nominal anual mes vencido de 12,6% a una tasa con nominalidad semestral.
\({i_{NAMV}} = 12,6\% \)
\({i_{NSMV}} = 12,6\% \left( {\frac{6}{{12}}} \right) = 6,3\%\)
Se multiplico por (6/12) porque caben 6 veces los meses en un semestre (Nominalidad de la tasa de interés final) y 12 veces los meses en un año (Nominalidad de la tasa de interés inicial)
Fórmula para el cambio de la periodicidad de tasas de interés (mensual, bimestral, anual, etcétera.)
Cuando se hace el cambio de periodicidad de tasas de interés, las tasas siempre serán del tipo efectivas y estarán en su forma vencida. Si esta condición no se tiene se debe hacer la conversión previa para poder realizar el cambio de periodicidad.
\({i_{{E_f}}} = {\left( {1 + {i_{{E_i}}}} \right)^{\left( {\frac{{{m_i}}}{{{m_f}}}} \right)}} - 1\)
Fórmula para cambio de periodicidad de tasas.
\({i_{{E_i}}}\), Tasa de interés efectiva inicial.
\({i_{{E_f}}}\), Tasa de interés efectiva final.
\({m_{i}}\), Número de veces que cabe la periodicidad en un año de la tasa efectiva inicial.
\({m_{f}}\), Número de veces que cabe la periodicidad en un año de la tasa efectiva final.
Ejemplo: Convertir una tasa 3% trimestral vencida a bimestral.
\({i_{TV}} = 3\% \)
\({i_{BV}} = {\left( {1 + 3\% } \right)^{\left( {\frac{4}{6}} \right)}} - 1 = 1,99\% \)
Se elevo a 4/6 porque caben 4 veces los trimestres (Periodicidad de la tasa de interés inicial) en un año y 6 veces los bimestres (Periodicidad de la tasa de interés final) en un año.
Fórmula para el cambio de la forma de tasas de interés (vencida y anticipada)
Cuando se hace el cambio de la forma, no se altera la periodicidad de las tasas y siempre serán del tipo efectivas nunca se usan estas fórmulas para hacer el cambio de forma de tasa del tipo nominal. Si esta condición no se tiene se debe hacer la conversión previa para poder realizar el cambio de la forma.
\({i_A} = \frac{{{i_V}}}{{\left( {\;1 + {i_V}} \right)}}\)
Fórmula para cambio de tasas vencidas a anticipadas.
\( {i_V} = \frac{{{i_A}}}{{\;\left( {1 - {i_A}} \right)}} \)
Fórmula para cambio de tasas anticipadas a vencidas.
\({i_{A}}\), Tasa de interés efectiva en su forma anticipada.
\({i_{V}}\), Tasa de interés efectiva en su forma vencida.
Ejemplo: Convertir una tasa trimestral vencida del 3% a trimestral anticipada.
\( {i_{TV}} = 3\% \)
\( {i_{TA}} = \frac{{3\% }}{{\;\left( {1 + 3\% } \right)}} = 2,91\% \)
Ambas tasas conservan la misma periodicidad trimestral y ambas tasas son efectivas.
En resumen, las fórmulas para cambio de tasas son las siguientes.
\({i_E} = \frac{{{i_N}}}{n}\)
Fórmula para cambio de tasas de nominal a efectiva.
\({i_N} = n{i_E}\)
Fórmula para cambio de tasas de efectiva a nominal.
\({i_{{N_f}}} = {i_{{N_i}}}\left( {\frac{{{n_f}}}{{{n_i}}}} \right)\)
Fórmula para cambio de nominalidad de tasas.
\({i_{{E_f}}} = {\left( {1 + {i_{{E_i}}}} \right)^{\left( {\frac{{{m_i}}}{{{m_f}}}} \right)}} - 1\)
Fórmula para cambio de periodicidad de tasas.
\({i_A} = \frac{{{i_V}}}{{\left( {\;1 + {i_V}} \right)}}\)
Fórmula para cambio de tasas vencidas a anticipadas.
\( {i_V} = \frac{{{i_A}}}{{\;\left( {1 - {i_A}} \right)}} \)
Fórmula para cambio de tasas anticipadas a vencidas.
\({i_{E}}\), Tasa de interés efectiva.
\({i_{N}}\), Tasa de interés nominal.
\({i_{{N_i}}}\), Tasa de interés nominal inicial.
\({i_{{N_f}}}\), Tasa de interés nominal final.
\({i_{{E_i}}}\), Tasa de interés efectiva inicial.
\({i_{{E_f}}}\), Tasa de interés efectiva final.
\({i_{A}}\), Tasa de interés efectiva en su forma anticipada.
\({i_{V}}\), Tasa de interés efectiva en su forma vencida.
\(n\), Número de veces que cabe la periodicidad en la nominalidad de la tasa nominal.
\({n_{i}}\), Número de veces que cabe la periodicidad en la nominalidad de la tasa nominal inicial.
\({n_{f}}\), Número de veces que cabe la periodicidad en la nominalidad de la tasa nominal final.
\({m_{i}}\), Número de veces que cabe la periodicidad en un año de la tasa efectiva inicial.
\({m_{f}}\), Número de veces que cabe la periodicidad en un año de la tasa efectiva final.
