Gradiente aritmético

El gradiente aritmético es una serie de pagos o retiros que se hacen con una periodicidad constante al inicio o al final de cada periodo y en donde cada pago o retiro va variando una cantidad constante "\(G\)", en cada periodo subsiguiente.

Las siguientes graficas muestran como es el perfil de un gradiente aritmético.

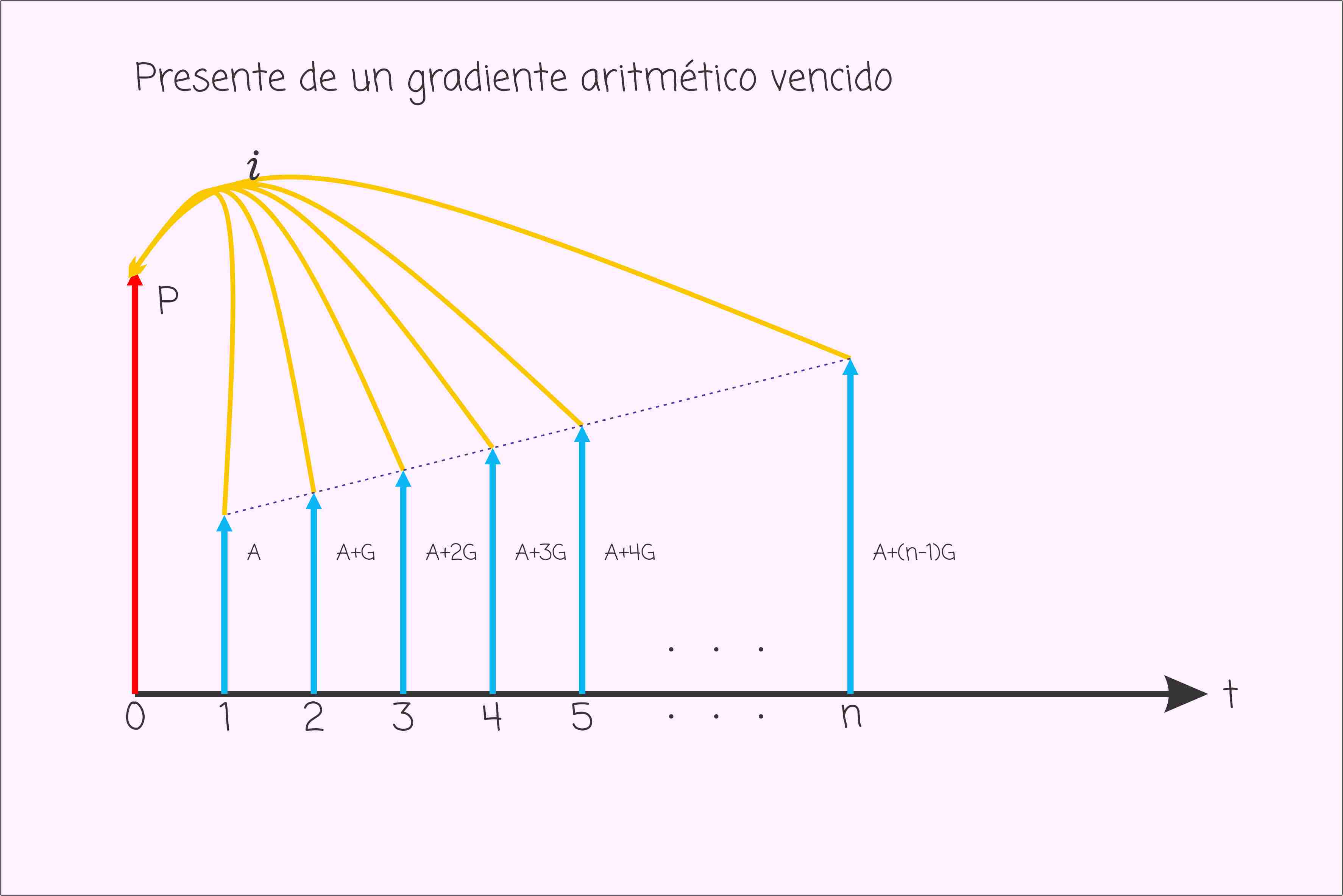
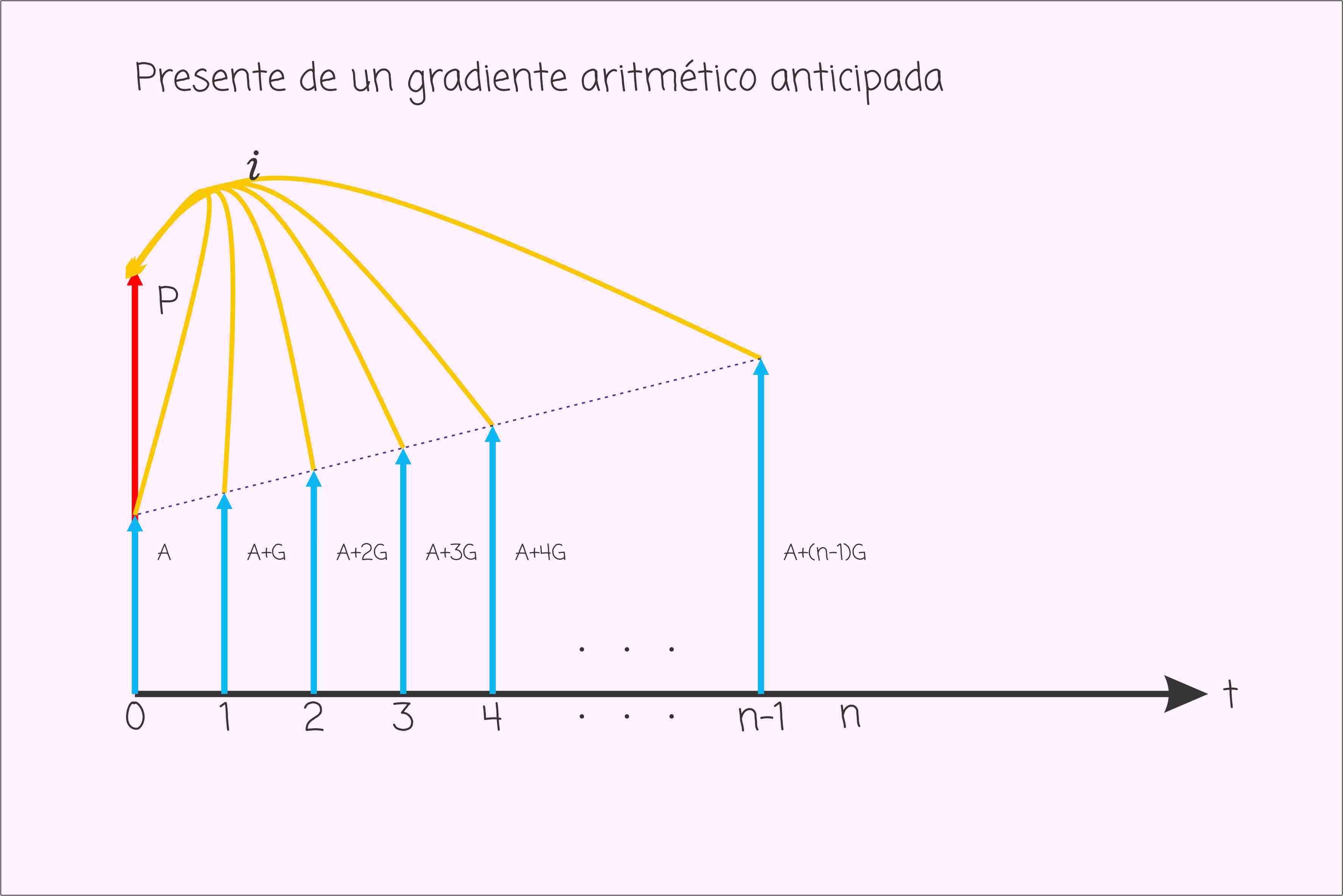
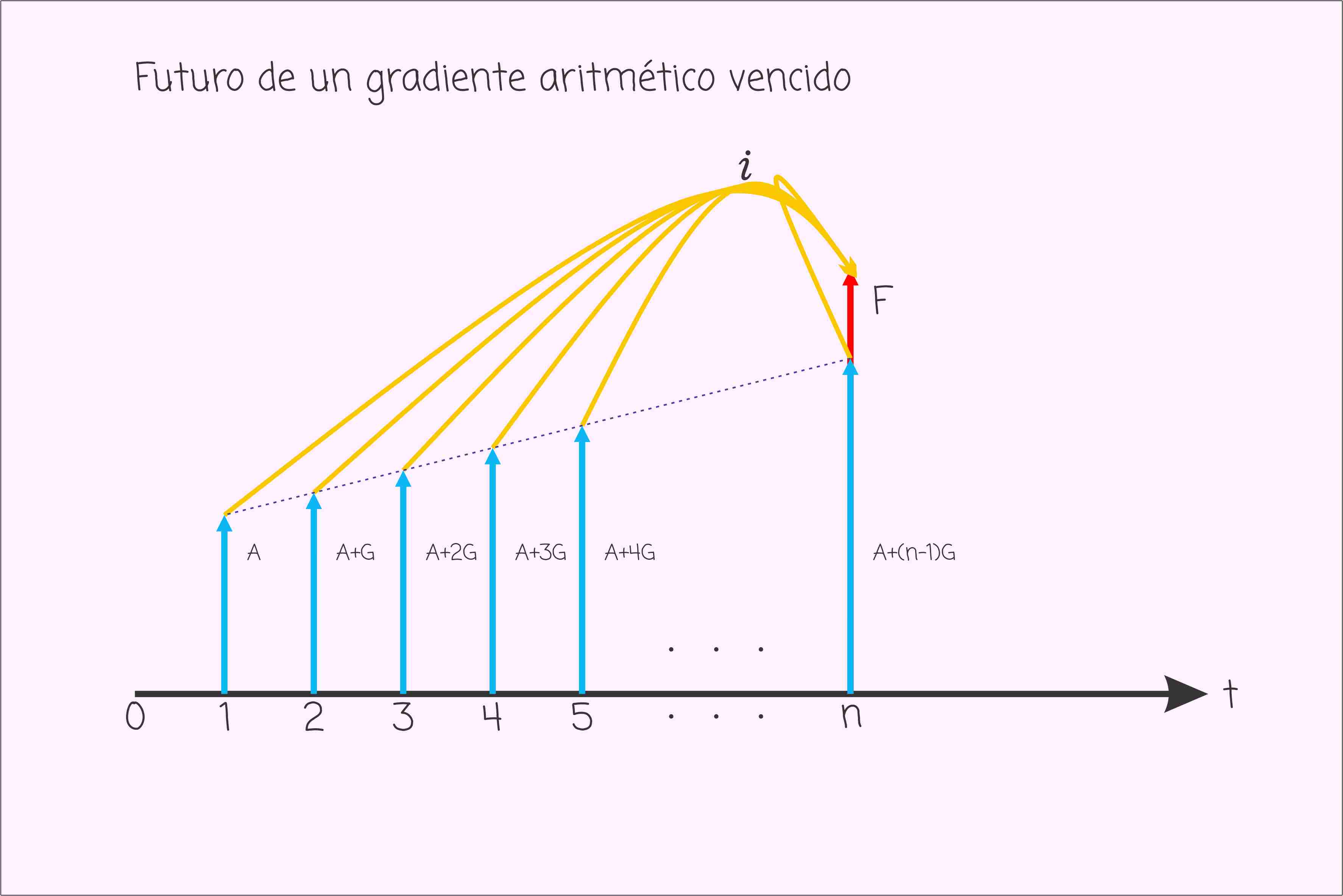
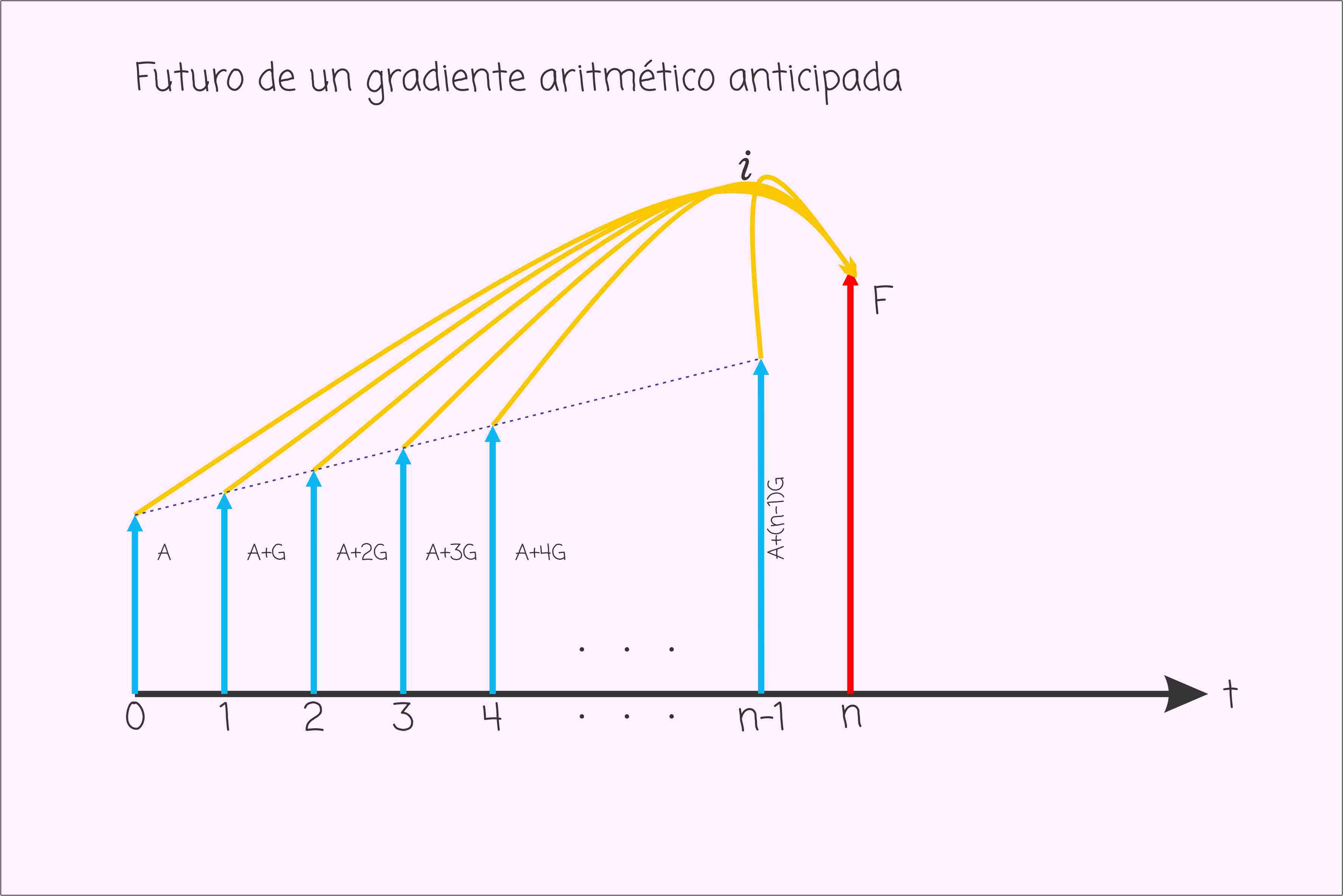
Valor presente de un gradiente aritmético

La siguiente formula representa el valor presente de un gradiente aritmético vencido, cabe recordar que para realizar este y los demás cálculos, la tasa de interés deber ser del tipo efectiva y estar en su forma vencida.

\(P = \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right]\)
Fórmula para valor presente de un gradiente aritmético vencido.

\( P = \left[ {\frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right]} \right]\left( {1 + i} \right) \)
Fórmula para valor presente de un gradiente aritmético anticipado.

\(P\), Valor presente.

\(A\), Valor del primer pago o retiro.

\(n\), Numero de periodos.

\(i\), Tasa de interés.

\(G\), Gradiente (Cantidad fija en moneda)

Valor futuro de un gradiente aritmético

La siguiente formula permite calcular el valor futuro del gradiente.

\( F = \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] \)
Fórmula para valor futuro de un gradiente aritmético vencido.

\( F = \left[ {\frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right]} \right]\left( {1 + i} \right) \)
Fórmula para valor futuro de un gradiente aritmético anticipado.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n\), Numero de periodos.

\(i\), Tasa de interés.

\(G\), Gradiente (Cantidad fija en moneda)

Valor del primer pago de un gradiente aritmético

El cálculo del primer pago de un gradiente aritmético, puede obtenerse tanto para el caso donde se tiene el valor presente o el valor futuro de dicho gradiente.

\( A = \frac{{i\left[ {P - \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right]} \right]}}{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}} \)
Fórmula para valor del primer pago de un gradiente aritmético vencido (Conociendo el valor presente).

\( A = \frac{{i\left[ {\frac{P}{{\left( {1 + i} \right)}} - \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right]} \right]}}{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}} \)
Fórmula para valor del primer pago de un gradiente aritmético anticipado (Conociendo el valor presente).

\( A = \frac{{i\left[ {F - \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right]} \right]}}{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}} \)
Fórmula para valor del primer pago de un gradiente aritmético vencido (Conociendo el valor futuro)

\( A = \frac{{i\left[ {\frac{F}{{\left( {1 + i} \right)}} - \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right]} \right]}}{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}} \)
Fórmula para valor del primer pago de un gradiente aritmético anticipado (Conociendo el valor futuro)

\(P\), Valor presente.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n\), Numero de periodos.

\(i\), Tasa de interés.

\(G\), Gradiente (Cantidad fija en moneda)

Número de periodos de un gradiente aritmético

No existe una manera analítica para obtener el número de periodos de un gradiente aritmético, por la misma complejidad de las fórmulas, es por esto que según los datos que se tengan se recomienda que simplemente se iguale a cero ya sea la fórmula de valor presente o valor futuro según sean los datos que se tengan e iterar el número de periodos para así obtener una respuesta a este valor, por lo general estas iteraciones se hacen en Excel ya que a mano resultaría realmente engorroso y no sería algo practico.

\( \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right] - P = 0 \)
Ecuación para número de periodos de un gradiente aritmético vencido (Iterar número de periodos - Conociendo el valor presente).

\( \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right] - \frac{P}{{\left( {1 + i} \right)}} = 0 \)
Ecuación para número de periodos de un gradiente aritmético anticipado (Iterar número de periodos - Conociendo el valor presente).

\( \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] - F = 0 \)
Ecuación para número de periodos de un gradiente aritmético vencido (Iterar número de periodos - Conociendo el valor futuro).

\( \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] - \frac{F}{{\left( {1 + i} \right)}} = 0 \)
Ecuación para número de periodos de un gradiente aritmético anticipado (Iterar número de periodos - Conociendo el valor futuro).

\(P\), Valor presente.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n\), Numero de periodos.

\(i\), Tasa de interés.

\(G\), Gradiente (Cantidad fija en moneda)

Tasa de interés de un gradiente aritmético

En este caso tampoco existe una forma analítica de obtener la tasa de interés, precisamente por la complejidad de la formula como se ha mencionado, igualmente lo que se hace es igualar a cero ya sea la formula de valor presente o la formula de valor futuro e iterar el valor de la tasa de interés hasta lograr satisfacer la ecuación. Las siguientes ecuaciones nos permite hallar la tasa al iterar esta.

\( \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right] - P = 0 \)
Ecuación para tasa de interés de un gradiente aritmético vencido (Iterar tasa de interés - Conociendo el valor presente).

\( \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right] - \frac{P}{{\left( {1 + i} \right)}} = 0 \)
Ecuación para tasa de interés de un gradiente aritmético anticipado (Iterar tasa de interés - Conociendo el valor presente).

\( \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] - F = 0 \)
Ecuación para tasa de interés de un gradiente aritmético vencido (Iterar tasa de interés - Conociendo el valor futuro).

\( \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] - \frac{F}{{\left( {1 + i} \right)}} = 0 \)
Ecuación para tasa de interés de un gradiente aritmético anticipado (Iterar tasa de interés - Conociendo el valor futuro).

\(P\), Valor presente.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n\), Numero de periodos.

\(i\), Tasa de interés.

\(G\), Gradiente (Cantidad fija en moneda)

Como se puede ver las ecuaciones para el numero de periodos y la tasa de interés son las mismas, lo único que cambio es lo que se está iterando, lo cual es el número de periodos o la tasa de interés.

Resumen de las fórmulas para gradiente aritmético.

\(P = \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right]\)
Fórmula para valor presente de un gradiente aritmético vencido.

\( P = \left[ {\frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right]} \right]\left( {1 + i} \right) \)
Fórmula para valor presente de un gradiente aritmético anticipado.

\( F = \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] \)
Fórmula para valor futuro de un gradiente aritmético vencido.

\( F = \left[ {\frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right]} \right]\left( {1 + i} \right) \)
Fórmula para valor futuro de un gradiente aritmético anticipado.

\( A = \frac{{i\left[ {P - \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right]} \right]}}{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}} \)
Fórmula para valor del primer pago de un gradiente aritmético vencido (Conociendo el valor presente).

\( A = \frac{{i\left[ {\frac{P}{{\left( {1 + i} \right)}} - \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right]} \right]}}{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}} \)
Fórmula para valor del primer pago de un gradiente aritmético anticipado (Conociendo el valor presente).

\( A = \frac{{i\left[ {F - \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right]} \right]}}{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}} \)
Fórmula para valor del primer pago de un gradiente aritmético vencido (Conociendo el valor futuro)

\( A = \frac{{i\left[ {\frac{F}{{\left( {1 + i} \right)}} - \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right]} \right]}}{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}} \)
Fórmula para valor del primer pago de un gradiente aritmético anticipado (Conociendo el valor futuro)

\( \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right] - P = 0 \)
Ecuación para número de periodos de un gradiente aritmético vencido (Iterar número de periodos - Conociendo el valor presente).

\( \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right] - \frac{P}{{\left( {1 + i} \right)}} = 0 \)
Ecuación para número de periodos de un gradiente aritmético anticipado (Iterar número de periodos - Conociendo el valor presente).

\( \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] - F = 0 \)
Ecuación para número de periodos de un gradiente aritmético vencido (Iterar número de periodos - Conociendo el valor futuro).

\( \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] - \frac{F}{{\left( {1 + i} \right)}} = 0 \)
Ecuación para número de periodos de un gradiente aritmético anticipado (Iterar número de periodos - Conociendo el valor futuro).

\( \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right] - P = 0 \)
Ecuación para tasa de interés de un gradiente aritmético vencido (Iterar tasa de interés - Conociendo el valor presente).

\( \frac{{A\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {1 - {{\left( {1 + i} \right)}^{ - n}}} \right]}}{i} - \frac{n}{{{{\left( {1 + i} \right)}^n}}}} \right] - \frac{P}{{\left( {1 + i} \right)}} = 0 \)
Ecuación para tasa de interés de un gradiente aritmético anticipado (Iterar tasa de interés - Conociendo el valor presente).

\( \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] - F = 0 \)
Ecuación para tasa de interés de un gradiente aritmético vencido (Iterar tasa de interés - Conociendo el valor futuro).

\( \frac{{A\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} + \left( {\frac{G}{i}} \right)\left[ {\frac{{\left[ {{{\left( {1 + i} \right)}^n} - 1} \right]}}{i} - n} \right] - \frac{F}{{\left( {1 + i} \right)}} = 0 \)
Ecuación para tasa de interés de un gradiente aritmético anticipado (Iterar tasa de interés - Conociendo el valor futuro).

\(P\), Valor presente.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n\), Numero de periodos.

\(i\), Tasa de interés.

\(G\), Gradiente (Cantidad fija en moneda)