Gradiente geométrico escalonado.

El gradiente geométrico escalonado es una serie de pagos o retiros que se hacen con una periodicidad constante al inicio o al final de cada periodo y en donde los pagos se mantienen constante durante otra cierta periodicidad pero que al cabo de esta otra cierta periodicidad el pago o retiro varia de una manera escalonada una proporción constante “G”, para luego permanecer constante nuevamente en cada una de esta otra cierta periodicidad subsiguiente

Las siguientes graficas muestran como es el perfil de un gradiente geométrico escalonado.

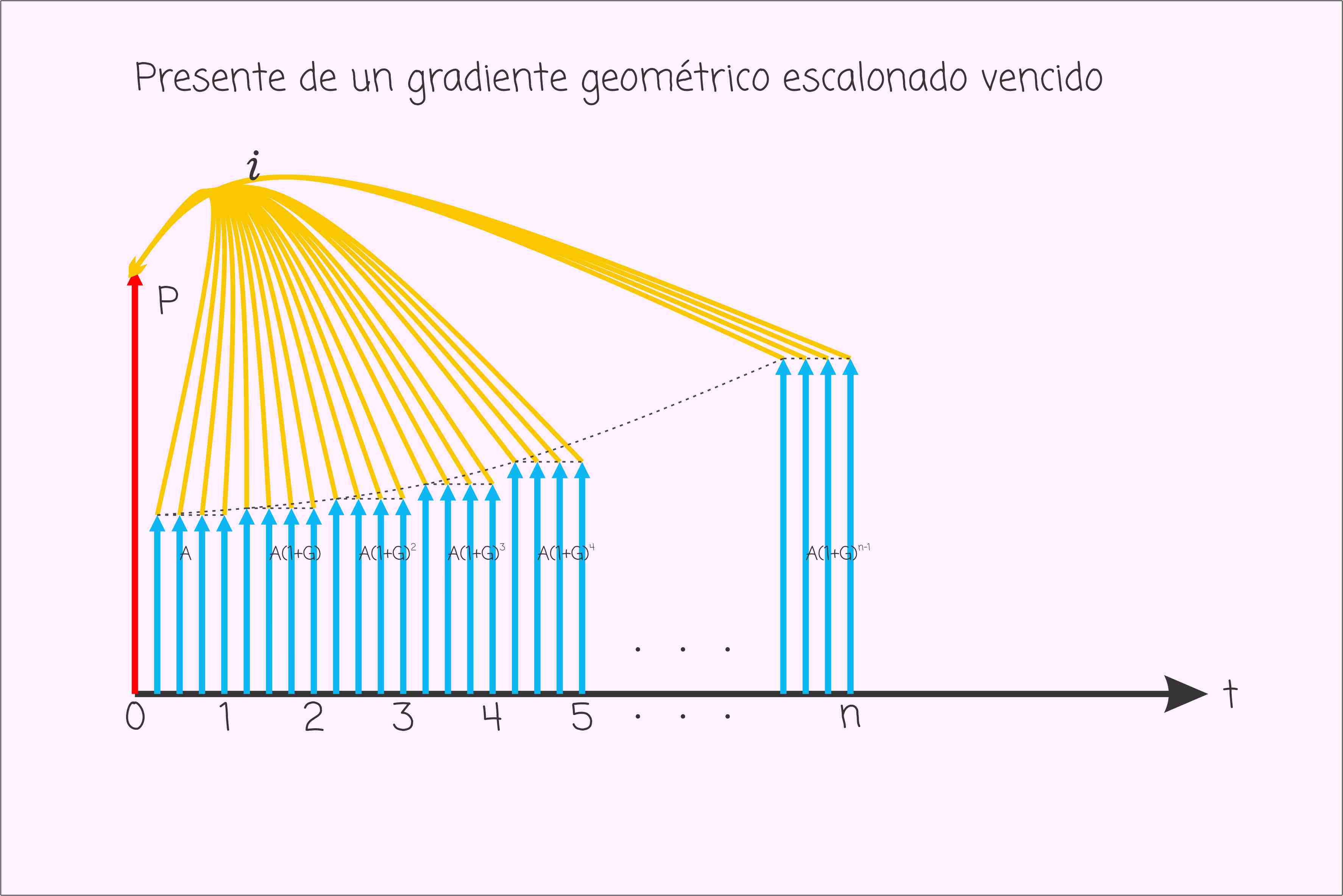
Como estas seria también resulta dispendiosa para manejarla de manera algebraica, para el cálculo del número de periodos y la tasa de interés solo se indicará la ecuación que se puede emplear y simplemente indicar que en estos casos se realiza la iteración respectiva del parámetro que se quiere hallar.

Valor presente de un gradiente geométrico escalonado.

El valor presente de un gradiente geométrico escalonado viene dado por las siguientes formulas, para los casos vencidos y anticipados.

\(P = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}\)
Fórmula para valor presente de un gradiente geométrico escalonado vencido.

\(P = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]\left( {1 + {i_1}} \right)}}{{\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}\)
Fórmula para valor presente de un gradiente geométrico escalonado anticipado.

\(P\), Valor presente.

\(A\), Valor del primer pago o retiro.

\(n_1\), Numero de periodos iguales que hay en cada periodo escalonado.

\(n_2\), Numero de periodos escalonados.

\(i_1\), Tasa de interés con la misma periodicidad de los pagos o retiros iguales.

\(i_2\), Tasa de interés con la misma periodicidad de los periodos escalonados.

\(G\), Gradiente (Cantidad fija en porcentaje)

Valor futuro de un gradiente geométrico escalonado.

El valor presente de un gradiente geométrico escalonado viene dado por las siguientes formulas, para los casos vencidos y anticipados.

\(F = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}}\)
Fórmula para valor futuro de un gradiente geométrico escalonado vencido.

\(F = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]\left( {1 + {i_1}} \right)}}{{\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}}\)
Fórmula para valor futuro de un gradiente geométrico escalonado anticipado.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n_1\), Numero de periodos iguales que hay en cada periodo escalonado.

\(n_2\), Numero de periodos escalonados.

\(i_1\), Tasa de interés con la misma periodicidad de los pagos o retiros iguales.

\(i_2\), Tasa de interés con la misma periodicidad de los periodos escalonados.

\(G\), Gradiente (Cantidad fija en porcentaje)

Valor del primer pago de un gradiente geométrico escalonado

Para hallar el valor del primer pago de un gradiente geométrico escalonado, se usan las siguientes formulas. Cualquiera que sea el escenario, vencido o anticipado, se puede obtener a través de alguna de las siguientes formulas.

\(A = \frac{{P\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]} \right]}}\)
Fórmula para valor del primer pago de un gradiente geométrico escalonado vencido (Conociendo el valor presente)

\(A = \frac{{P\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]\left( {1 + {i_1}} \right)} \right]}}\)
Fórmula para valor del primer pago de un gradiente geométrico escalonado anticipado (Conociendo el valor presente)

\(A = \frac{{F\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}}{{\left[ {\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]} \right]}}\)
Fórmula para valor del primer pago de un gradiente geométrico escalonado vencido (Conociendo el valor futuro)

\(A = \frac{{F\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}}{{\left[ {\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]\left( {1 + {i_1}} \right)} \right]}}\)
Fórmula para valor del primer pago de un gradiente geométrico escalonado anticipado (Conociendo el valor futuro)

\(P\), Valor presente.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n_1\), Numero de periodos iguales que hay en cada periodo escalonado.

\(n_2\), Numero de periodos escalonados.

\(i_1\), Tasa de interés con la misma periodicidad de los pagos o retiros iguales.

\(i_2\), Tasa de interés con la misma periodicidad de los periodos escalonados.

\(G\), Gradiente (Cantidad fija en porcentaje)

Numero de periodos o tasa de interés de un gradiente geométrico escalonado

En este caso también resulta conveniente usar la ecuación de valor presente o futuro según la información que se tenga y proceder a iterar para obtener el valor que se requiere.

\(\frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}} - P = 0\)
Ecuación para número de periodos o tasa de interés de un gradiente geométrico escalonado vencido (Conociendo el valor presente)

\(\frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}} - \frac{P}{{\left( {1 + {i_1}} \right)}} = 0\)
Ecuación para número de periodos o tasa de interés de un gradiente geométrico escalonado anticipado (Conociendo el valor presente)

\(\frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}} - F = 0\)
Ecuación para número de periodos o tasa de interés de un gradiente geométrico escalonado vencido (Conociendo el valor futuro)

\(\frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}} - \frac{F}{{\left( {1 + {i_1}} \right)}} = 0\)
Ecuación para número de periodos o tasa de interés de un gradiente geométrico escalonado anticipado (Conociendo el valor futuro)

\(P\), Valor presente.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n_1\), Numero de periodos iguales que hay en cada periodo escalonado.

\(n_2\), Numero de periodos escalonados.

\(i_1\), Tasa de interés con la misma periodicidad de los pagos o retiros iguales.

\(i_2\), Tasa de interés con la misma periodicidad de los periodos escalonados.

\(G\), Gradiente (Cantidad fija en porcentaje)

Resumen fórmulas para gradiente geométrico escalonado

\(P = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}\)
Fórmula para valor presente de un gradiente geométrico escalonado vencido.

\(P = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]\left( {1 + {i_1}} \right)}}{{\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}\)
Fórmula para valor presente de un gradiente geométrico escalonado anticipado.

\(F = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}}\)
Fórmula para valor futuro de un gradiente geométrico escalonado vencido.

\(F = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]\left( {1 + {i_1}} \right)}}{{\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}}\)
Fórmula para valor futuro de un gradiente geométrico escalonado anticipado.

\(A = \frac{{P\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]} \right]}}\)
Fórmula para valor del primer pago de un gradiente geométrico escalonado vencido (Conociendo el valor presente)

\(A = \frac{{P\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]\left( {1 + {i_1}} \right)} \right]}}\)
Fórmula para valor del primer pago de un gradiente geométrico escalonado anticipado (Conociendo el valor presente)

\(A = \frac{{F\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}}{{\left[ {\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]} \right]}}\)
Fórmula para valor del primer pago de un gradiente geométrico escalonado vencido (Conociendo el valor futuro)

\(A = \frac{{F\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}}{{\left[ {\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]\left( {1 + {i_1}} \right)} \right]}}\)
Fórmula para valor del primer pago de un gradiente geométrico escalonado anticipado (Conociendo el valor futuro)

\(\frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}} - P = 0\)
Ecuación para número de periodos o tasa de interés de un gradiente geométrico escalonado vencido (Conociendo el valor presente)

\(\frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right){{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}} - \frac{P}{{\left( {1 + {i_1}} \right)}} = 0\)
Ecuación para número de periodos o tasa de interés de un gradiente geométrico escalonado anticipado (Conociendo el valor presente)

\(\frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}} - F = 0\)
Ecuación para número de periodos o tasa de interés de un gradiente geométrico escalonado vencido (Conociendo el valor futuro)

\(\frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]\left[ {{{\left( {1 + G} \right)}^{{n_2}}} - {{\left( {1 + {i_2}} \right)}^{{n_2}}}} \right]}}{{\left[ {{i_1}\left( {G - {i_2}} \right)} \right]}} - \frac{F}{{\left( {1 + {i_1}} \right)}} = 0\)
Ecuación para número de periodos o tasa de interés de un gradiente geométrico escalonado anticipado (Conociendo el valor futuro)

\(P\), Valor presente.

\(F\), Valor futuro.

\(A\), Valor del primer pago o retiro.

\(n_1\), Numero de periodos iguales que hay en cada periodo escalonado.

\(n_2\), Numero de periodos escalonados.

\(i_1\), Tasa de interés con la misma periodicidad de los pagos o retiros iguales.

\(i_2\), Tasa de interés con la misma periodicidad de los periodos escalonados.

\(G\), Gradiente (Cantidad fija en porcentaje)

Caso especial cuando "\( G=i_2 \)."

También podríamos tener el caso en el cual el gradiente escalonado sea igual a la tasa de interés periódica de los periodos. El valor presente de este gradiente es el siguiente.

\( P = \frac{{A\left[ {{{\left( {1 + {i_1}} \right)}^{{n_1}}} - 1\;} \right]{n_2}}}{{\left[ {{i_1}\left( {1 + {i_2}} \right)} \right]}} \)
Fórmula para valor presente de un gradiente geométrico escalonado vencido \( G=i_2 \)

\(P\), Valor presente.

\(A\), Valor del primer pago o retiro.

\(n_1\), Numero de periodos iguales que hay en cada periodo escalonado.

\(n_2\), Numero de periodos escalonados.

\(i_1\), Tasa de interés con la misma periodicidad de los pagos o retiros iguales.

\(i_2\), Tasa de interés con la misma periodicidad de los periodos escalonados.

No se analizan los casos de valor futuro, el número de periodo o tasa de interés ya que este caso especial es prácticamente imposible que se estudie, solo se deja como un caso especial que existe, y en caso de que se quiera obtener cualquiera de los otros parámetros ya tocaría despejarlo o si es el caso del valor futuro, seria llevar este valor presente a un valor futuro.